Today, the schedule was switched around a bit from what I've gotten used to. (I know, it's only been two days. I can't really pretend that I'm used to a set routine and be upset when they change it. But still...) Rather than beginning with a short course, we began with the research seminar.
Today picked up about where we'd lft off yesterday. Only instead of working with the lemma that he'd told us we should consider proving (and done in the review session,) Dr. Farley gave us a new, slightly more helpful, lemma nad proved it for us. (There were a lot of proofs today, which made me happy.) We then did a few more examples of groups and their presentations, though the examples were a bit rambling and difficult to follow. Particularly when he tried to give an example of an infinite group.
Suppose you have a 45-45-90 triangle. You can label each side “a,” “b,” or “c” with “a” and “b” being legs and “c” being the hypotenuse, and define operations based on flipping over sides. By repeating this sucessively and waving your hands a lot, you can prove that the this tiles the plate.
To be able to say anything about this, we needed to back up and get a new theorem. This one had such strong conitions it was hard to imagine it ever being applicable, but apparently it is sometimes. What time it was was left a bit unclear, as the example turned out not to work. But we did get an interesting detour into orbits and stabilizers, which we'd discussed for about half a day in my Abstract 1 class. (Add that to the list of topics I find interesting and want to learn about in more detail.)
So Dr. Farley waved his hands at the group on the board some more, we got the stbalizers of it to use in the lemma, he waved his hands some more, and we ended up with a homomorphism from the free group onto the group generated by flips of a, b, and c. Yay!
The next theorem also included a fair amount of hand wavin and lack of formal definitions. In short, it said that given any group presentation, we can build a topological space (specifically, a 2-complex) which had a fundamental group isomorphic to to the group given by the presentation. The proof would be constructive, but we skimmed over a lot of the details of building it, and skimmed even more over the Seifer-van Kampen theorem to determine that the fundamental group of that space was in fact the group we'd been discussing earlier.
The idea behind the construction was a bit difficult to wrap my head around (“You might be tempted to try and visualize this. It won't work.”) However, I could see generally how, if I knew more about topology, I might be able to believe it. So every group that can be represented by a group presentaiton is isomorphic fundamental group of a topological space. However, from yesterday, we knew that every group is isomorphic to a group determined by its presentation. So by transitivity, we know every group is isomorphic to a fundamental group. Which just confirms something I'd long believed: algebraists abuse the term “fundamental.”
Up until Abstract Algebra, you only really encounter a couple of fundamental thoerems. Arithmatic. Algebra. Calculus. Each of those are extremely important and distinctive. You learn a lot of theorems, but only a couple of fundmaental theorems.
And then you reach Abstract Algebra, and it seems like every other chapter has a fundamental theorem. The Fundamental Theorem of Cyclic Groups. Fundamental Theorem of Group Homomorphisms. The Fundamental Theorem of Groups. (Sometimes called the Fundamental Theorem of Finite Abelian Groups, which is just redundant. If a group weren't finite, it wouldn't be Abelian.)
But the theorems weren't enough. No. Nor is it even enough to have a special class of fundamental groups. No. You need to prove that every group is isomorphic to a fundamental group. Every group is ssuper-important!
After the last few hand-waviy proofs, we went into a theorem that was given with no proof at all. The theorem was that there exist presentations such that both the generating set S and the relators R are finite in number, but there is no algorithm to determine whether a word is in the nomral closure of R in S.
This of course begs of the question of if it's still possible to make sense out of groups based on the presentations. Which leads to the combinatorial approach and the geometric approach. Dr. Farley skimmed over the first to focus on the second.And I perked up in the hopes that, after 8 hours of research seminar, he would finally get around to describing the problems.
He didn't, but he did describe the next best thing- graphs!
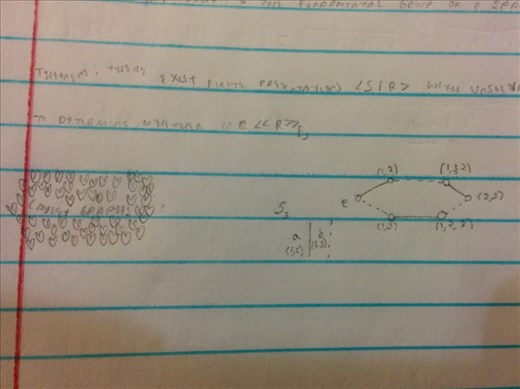
Ever since he'd started talking about group presentations on Monday, I'd been hoping that we would get around to Cayley Graphs. It makes all the work we did with generators and relators more relevant (The process for drawing a graph depends on the graph having a presentation.) We only had time to do one example (S_3, which has been our standard group for the research seminar. It doesn't have the most interesting Cayley Graph, unfrotunately.) He drew the example on the board, then stepped back and looked at it for a little bit. “Maybe I should have begun with that.” It probably would have made things clearer.
Once I figure out how topology and fundamental groups relate to Cayley Graphs, and what this all has to do with research, everything should hopefully make more sense.
Speaking of making sense... after the second research seminar (one before lunch, one after) we had the analysis short course. Today's class was focused on counting and cardinality. Still mainly review from the semester of Real Analysis, but still interestinng ideas, and cool proofs.
By the time we finished, it was a little after 5 o'clock. We all kind of mean to check out the B.E.S.T. Library (Business, Engineering, Science, and Technnology. Also contains math books), but haven't quite gotten around to it. It closes at 6, which means going either during the day or right after classes end, and no one really wants to do that. So it's high on my to-do list, but who knows when I'll get around to it.
Around 6:30 we went to dinner, and then from there back to the dorms to play Moving Man's Rummy. I got a third deck shuffled in, which had the advantage of stopping us from running out, but the disadvantage of being a pain to shuffle, and even worse to separate. We played a few rounds, then decided the room (the lounge in Elliot. It was larger and less smelly than the lounge in Stoddard) wasn't getting any cooler, so we went to Armstrong, which was pleasantly air conditioned. There weren't quite enough people to play Mafia, so we ended up playing the old-fashioned game of talking. More specifically, posing and answering questions. There were some interesting questions and even more interesting responses, and it was nice way to get to know each other a bit better.
We stayed in the building until they were about to kick us out, then separated and returned to our dorms. Around 11, we had a Taylor Swift Dance Party. By which I mean we played music and tried to block open the doors of our rooms. It took me almost the entire song to realize that a stack of 20 books wasn't enough to block the door open- I needed to wedge a shoe underneath it and then use some boogs to stop the shoe from moving. After that, we stood out in the hallway while Delaney briefly described the fun and terribleness that was her second degree black belt test. Then we went back to our rooms or the lounge for bed or blogging (or cross-stitching).
And with that, the first week was half over.